Ekuivalensi Antar Deterministic Finite Automata
Materi 4
EKUIVALENSI ANTAR DETERMINISTIC FINITE AUTOMATA
Sasaran kita di sini adalah mengurangi jumlah state dari suatu Finite State Automata, dengan tidak mengurangi kemampuannya semula untuk menerima suatu bahasa.
Ada dua buah istilah baru yang perlu kita ketahui yaitu :
- Distinguishable: yang berartu dapat dibedakan
- Indistinguishable: yang berarti tidak dapat dibedakan
Reduksi dilakukan untuk mengurangi jumlah state tanpa mengurangi kemampuan untuk menerima suatu bahasa seperti semula (efesiensi). State pada FSA dapat direduksi apabila terdapat useless state. Hasil dari FSA yang direduksi merupakan ekivalensi dari FSA semula.
Pasangan State dapat dikelompokkan berdasarkan:
- Distinguishable State (dapat dibedakan)
- Dua state p dan q dari suatu DFA dikatakan indistinguisable apabila:
- δ(q,w) ∈ F dan δ(p,w) ∈ F atau δ(q,w) ∉ F dan δ(p,w) ∉ F
- untuk semua w ∊ S*
- Indistinguishable State (tidak dapat dibedakan)
- Dua state p dan q daru suatu DFA dikatakan distinguishable jika ada string w ∊ S* hungga:
- δ(q,w) ∈ F dan δ(p,w) ∉ F
2. Reduksi Jumlag State Pada FSA-Relasi
Pasangan dua buah state memiliki salah satu kemungkinan : distinguishable atau indistinguishable tetapi tidak kedua-duanya. Dalam hal ini terdapat sebuah relasi :
- Jika p dan q indistinguishable,
- dan q dan r indistinguishable
- maka p, r indistinguishable dan
- p,q,r indistinguishable
Dalam melakukan eveluasi state, didefinisikan suatu relasi : Untuk Q yg merupakan himpunan semua state
- D adalah himpunan state-state distinguishable, dimana D ⊆ Q
- N adalah himpunan state-state indistinguishable, dimana N ⊆ Q
- maka x ∈ N jika x ∈ Q dan x ∉ D
Sebuah Mesin DFA
Lakukan reduksi state pada DFA dibawah ini?
Reduksi Jumlah State Pada FSA – Step
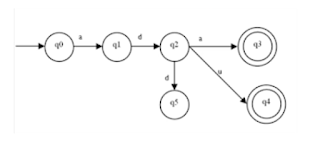
- State q5 tidak dapat dicapai dari state awal dengan jalan apapun (useless state). Hapus state q5
- Catat state-state distinguishable, yaitu : q4 ⊄ F sedang q0, q1, q2, q3 ⊄ F sehingga pasangan Pasangan State :
(q0,q1)(q0,q2)(q0,q3)(q0,q4)(q1,q2)(q1,q3)(q1,q4)(q2,q3)(q2,q4)(q3,q4)
Pasangan State :
(q0,q1)(q0,q2)(q0,q3)(q0,q4) → Distinguisable(q1,q2)(q1,q3)(q1,q4) → Distinguisable(q2,q3)(q2,q4) → Distinguisable(q3,q4) → Distinguisable
Pasangan State :
(q0,q1) → Distinguisable(q0,q2)
(q0,q3)(q0,q4) → Distinguisable(q1,q2)(q1,q3)(q1,q4) → Distinguisable(q2,q3)(q2,q4) → Distinguisable(q3,q4) → Distinguisable
Cari Status Pasangan lainnya, dengan memperhatikan inputan yang tersedia yaitu 0 dan 1 :
- Pasangan (q0,q1)
- δ(q0, 0) = q1 dan δ(q1, 0) = q2 ➔ (q1 , q2) belum terdefinisi
- δ(q0, 1) = q3 dan δ(q1, 1) = q4 ➔ (q3 , q4) Distinguisable
Maka (q0,q1) adalah Distingushable
Pasangan State :
(q0,q1) → Distinguisable(q0,q2) → Distinguisable
(q0,q3)(q0,q4) → Distinguisable(q1,q2)(q1,q3)(q1,q4) → Distinguisable(q2,q3)(q2,q4) → Distinguisable(q3,q4) → Distinguisable
- Pasangan (q0,q1)
- δ(q0, 0) = q1 dan δ(q2, 0) = q1 ➔ (q1 , q1) belum terdefinisi
- δ(q0, 1) = q3 dan δ(q2, 1) = q4 ➔ (q3 , q4) Distinguisable
Maka (q0,q2) adalah Distingushable
Pasangan State :
(q0,q1) → Distinguisable(q0,q2) → Distinguisable
(q0,q3) → Distinguisable(q0,q4) → Distinguisable(q1,q2)(q1,q3)(q1,q4) → Distinguisable(q2,q3)(q2,q4) → Distinguisable
(q3,q4) → Distinguisable
- Pasangan (q0,q1)
- δ(q0, 0) = q1 dan δ(q3, 0) = q2 ➔ (q1 , q2) belum terdefinisi
- δ(q0, 1) = q3 dan δ(q3, 1) = q4 ➔ (q3 , q4) Distinguisable
Maka (q0,q3) adalah Distingushable
Pasangan State :
(q0,q1) → Distinguisable(q0,q2) → Distinguisable
(q0,q3) → Distinguisable(q0,q4) → Distinguisable(q1,q2) → Belum terdefinisi(q1,q3)(q1,q4) → Distinguisable(q2,q3)(q2,q4) → Distinguisable
(q3,q4) → Distinguisable
- Pasangan (q0,q1)
- δ(q1, 0) = q2 dan δ(q2, 0) = q1 ➔ (q2 , q1) belum terdefinisi
- δ(q1, 1) = q4 dan δ(q2, 1) = q4 ➔ (q4 , q4) belum terdefinisi
Maka (q1,q2) adalah Distingushable
Pasangan State :
(q0,q1) → Distinguisable(q0,q2) → Distinguisable
(q0,q3) → Distinguisable(q0,q4) → Distinguisable(q1,q2) → Belum terdefinisi(q1,q3) → Belum terdefinisi(q1,q4) → Distinguisable(q2,q3)(q2,q4) → Distinguisable
(q3,q4) → Distinguisable
- Pasangan (q0,q1)
- δ(q1, 0) = q2 dan δ(q3, 0) = q2 ➔ (q2 , q2) belum terdefinisi
- δ(q1, 1) = q4 dan δ(q3, 1) = q4 ➔ (q4 , q4) belum terdefinisi
Maka (q1,q3) adalah Distingushable
Pasangan State :
(q0,q1) → Distinguisable(q0,q2) → Distinguisable
(q0,q3) → Distinguisable(q0,q4) → Distinguisable(q1,q2) → Belum terdefinisi(q1,q3) → Belum terdefinisi(q1,q4) → Distinguisable(q2,q3) → Belum terdefinisi(q2,q4) → Distinguisable
(q3,q4) → Distinguisable
- Pasangan (q0,q1)
- δ(q2, 0) = q1 dan δ(q3, 0) = q2 ➔ (q1 , q2) belum terdefinisi
- δ(q2, 1) = q4 dan δ(q3, 1) = q4 ➔ (q4 , q4) belum terdefinisi
Maka (q1,q3) adalah Distingushable
Pasangan State :
(q0,q1) → Distinguisable(q0,q2) → Distinguisable
(q0,q3) → Distinguisable(q0,q4) → Distinguisable(q1,q2) → Belum terdefinisi(q1,q3) → Belum terdefinisi(q1,q4) → Distinguisable(q2,q3) → Belum terdefinisi(q2,q4) → Distinguisable
(q3,q4) → Distinguisable
Setelah semua pasangan state telah dipasangkan dengan setiap input yang ada maka terdapat state-state yang Distinguishable yaitu :
(q0,q1)(q0,q2)
(q0,q3)(q0,q4)(q1,q4)(q2,q4)
(q3,q4)
Karena berdasarkan relasi-relasi yang ada, tidak dapat dibuktikan (q1, q2), (q1, q3) dan (q2, q3) distinguishable, sehingga disimpulkan pasangan-pasangan state tersebut indistinguishable
Pasangan State :
(q0,q1) → Distinguisable(q0,q2) → Distinguisable
(q0,q3) → Distinguisable(q0,q4) → Distinguisable(q1,q2) → Belum terdefinisi(q1,q3) → Belum terdefinisi(q1,q4) → Distinguisable(q2,q3) → Belum terdefinisi(q2,q4) → Distinguisable
(q3,q4) → Distinguisable
Karena q1 indistinguishable dengan q2,
q1 indistinguishable dengan q3,
q2 indistinguishable dengan q3,
maka dapat disimpulkan q1, q2, q3 saling indistinguishable dan dapat dijadikan satu state.
Berdasarkan hasil diatas maka hasil dari DFA yang direduksi menjadi :
Komentar
Posting Komentar